Đây là một bài toán hay được chọn lọc .
Cho bảng  các ô vuông với
các ô vuông với 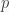 hàng và
hàng và  cột . Mỗi ô được đánh một số nguyên dương nào đó sao cho trên bảng không có hai số nào bằng nhau . Cho hai số nguyên dương
cột . Mỗi ô được đánh một số nguyên dương nào đó sao cho trên bảng không có hai số nào bằng nhau . Cho hai số nguyên dương  thỏa mãn
thỏa mãn  . Một số trên bảng được gọi là số xấu nếu số được đánh dấu ở ô đó nhỏ hơn ít nhất
. Một số trên bảng được gọi là số xấu nếu số được đánh dấu ở ô đó nhỏ hơn ít nhất  số cùng hàng và nhỏ hơn ít nhất
số cùng hàng và nhỏ hơn ít nhất 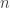 số cùng cột . Gọi
số cùng cột . Gọi  là tất cả các số xấu trên bảng . Tìm
là tất cả các số xấu trên bảng . Tìm 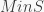 với mọi
với mọi  .
.
Chứng minh :
Trước hết ta sắp xếp 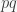 các nguyên dương
các nguyên dương  với
với 
Ở hàng thứ nhất xếp các số 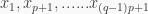
Ở hàng thứ hai xếp các số 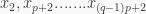
……
Ở hàng thứ 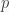 ta xếp các số
ta xếp các số 
Rõ ràng bảng này thỏa mãn 
Ta chứng minh đây là giá trị cần tìm .
Trước hết nếu 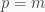 hoặc
hoặc  thì bài toán hiển nhiên đúng nên ở đây ta xét cho
thì bài toán hiển nhiên đúng nên ở đây ta xét cho  và
và 
Ý tưởng chính ở đây là quy nạp theo số 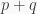
Nếu  thì hiển nhiên
thì hiển nhiên  và bài toán đang xét trở nên hiển nhiên
và bài toán đang xét trở nên hiển nhiên
Tất nhiên ta có thể dễ dàng kiểm tra một số trường hợp đầu tiên
Giả sử khẳng định đúng với 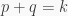 ta chứng minh đúng với
ta chứng minh đúng với 
Định nghĩa :
Một ô được gọi là xấu theo hàng nếu số được đánh ở ô đó nhỏ hơn ít nhất  số được đánh cùng hàng , tương tự cho ô xấu theo cột là ô nhỏ hơn ít nhất
số được đánh cùng hàng , tương tự cho ô xấu theo cột là ô nhỏ hơn ít nhất  số cùng cột
số cùng cột
Xét hàng thứ  bất kỳ trên bảng này .Ta kiểm tra được nó có
bất kỳ trên bảng này .Ta kiểm tra được nó có  ô là xấu theo hàng .
ô là xấu theo hàng .
Vậy trên mỗi hàng ,cột bất kỳ thì có  ô xấu theo hàng và
ô xấu theo hàng và  ô là xấu theo cột .
ô là xấu theo cột .
Nếu mỗi ô xấu theo hàng trùng với một ô xấu theo cột . Rõ ràng ta có

Vì vậy ta quan tâm đến các trường hợp mà một ô chỉ xấu theo hàng hoặc chỉ xấu theo cột .
Gọi  là số xấu theo hàng hoặc xấu theo cột nhỏ nhất trên bảng này
là số xấu theo hàng hoặc xấu theo cột nhỏ nhất trên bảng này
Không mất tỉnh tổng quát giả sử  nằm ở ô xấu theo hàng ( rõ ràng nó không xấu theo cột )
nằm ở ô xấu theo hàng ( rõ ràng nó không xấu theo cột )
Xét cột chứa số  trên bảng này
trên bảng này
Hiển nhiên ta dễ dàng chứng minh được 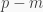 ô xấu theo cột trong cột chứa số
ô xấu theo cột trong cột chứa số  cũng là các ô xấu của bảng
cũng là các ô xấu của bảng 
Bỏ đi cột chứa số  ta có bảng
ta có bảng 
Rõ ràng theo giả thiết quy nạp thì 
Nên 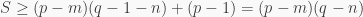
Bài toán được cm .
Giờ ta có một bài toán họ hàng với bài toán trên .
Cho  em trên sân trường . Ta gọi khoảng cách giữa hai em
em trên sân trường . Ta gọi khoảng cách giữa hai em 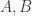 là
là 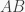 . Biết rằng nếu
. Biết rằng nếu 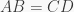 khi và chỉ khi
khi và chỉ khi  là hoán vị của
là hoán vị của  .
.
Sau khi có hiệu lệnh mỗi em cầm một khẩu súng nước trên tay , bắn vào người đứng gần mình nhất . Sau khi kết thúc người không bị bắn là người thắng .
Tìm tất cả các số nguyên dương  để bảo đảm luôn có ít nhất một em là người thắng với mọi cách xếp trên sân .
để bảo đảm luôn có ít nhất một em là người thắng với mọi cách xếp trên sân .
Chứng minh
Ta sẽ xét  là số lẻ . Nó chính là đáp số bài toán , trong trường hợp
là số lẻ . Nó chính là đáp số bài toán , trong trường hợp  chẵn sẽ dễ dàng có ví dụ bác bỏ .
chẵn sẽ dễ dàng có ví dụ bác bỏ .
Đặt  với
với  là một số nguyên dương .
là một số nguyên dương .
Quy nạp theo  . Với
. Với  thì khẳng định hiển nhiên đúng .
thì khẳng định hiển nhiên đúng .
Giả sử nó đúng với 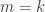 , khi
, khi  thì
thì 
Chọn ra hai em 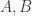 sao cho
sao cho 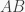 là khoảng cách ngắn nhất giữa em bất kỳ .
là khoảng cách ngắn nhất giữa em bất kỳ .
Xét tất cả các em còn lại giả sử là 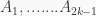
Theo quy nạp trong số các em này có một em 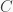 là thắng
là thắng
Xét tam giác 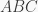 có
có 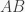 nhỏ nhất .
nhỏ nhất .
Ta có  không bắn vào
không bắn vào 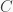 và
và 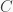 lại thắng ở
lại thắng ở 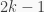 người kia nên
người kia nên 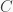 là thắng .
là thắng .
Bài toán được giải quyết .
Một bài toán khác trong ba bài toán hôm nay tôi muốn nói đến
Cho bảng vuông 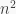 . Mỗi ô trên bảng ta đánh một số
. Mỗi ô trên bảng ta đánh một số 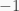 hoăc là
hoăc là  . Lần lượt gọi
. Lần lượt gọi  là tích tất cả các ô trên hàng
là tích tất cả các ô trên hàng  và cột
và cột  .
.
Tồn tại hay không cách đánh số thỏa 
Giải :
Câu trả lời là không tồn tại . Sau đây là chứng minh .
Phản chứng giả sử tồn tại cách đánh như vậy .
Lần lượt trên hàng và cột  gọi
gọi  là số các số
là số các số 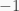 ở đó
ở đó
Hiển nhiên ta có 
Ta lại có
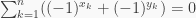
Với mọi  thì
thì 
Gọi  là số các số
là số các số  làm cho
làm cho 
Gọi 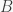 là số các số
là số các số  mà
mà 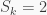
Gọi 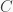 là số các số
là số các số  mà
mà 
Khi đó hiển nhiên  nên
nên 
Và hiển nhiên tổng 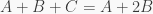 phải là số lẻ . (1)
phải là số lẻ . (1)
Ta có đánh giá sau , gọi  là số các số
là số các số 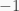 trên cả bảng
trên cả bảng
Khi đó ta có 
Với cách gọi trên ta thấy
 chính là số các bộ
chính là số các bộ 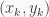 mà gồm , một chẵn một lẻ , hai chẵn , hai lẻ .
mà gồm , một chẵn một lẻ , hai chẵn , hai lẻ .
Cũng từ đánh giá trên ta có
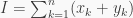 là số chẵn
là số chẵn
Nhận thấy 
Trong đó 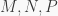 lần lượt là các giá trị
lần lượt là các giá trị 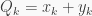 gồm , một chẵn một lẻ , hai chẵn , hai lẻ.
gồm , một chẵn một lẻ , hai chẵn , hai lẻ.
Rõ ràng ta có 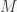 phải là số lẻ theo (1) , và
phải là số lẻ theo (1) , và 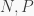 hiển nhiên chẵn
hiển nhiên chẵn
Từ các đó cho ta điều vô lý , ta có điều phải chứng minh .
thỏa mãn
với
và
là một hàm thực khả vi cấp hai thỏa mãn
và